Publicerad den 4 juli 2021
Modern medicinsk vetenskap förlitar sig i stor utsträckning på slutsatser dragna utifrån statistik. Två viktiga krav är att urvalet i studien är representativt för den population som man undersöker och att det är tillräckligt stort för att man med statistisk säkerhet skall kunna påvisa skillnader eller samband. Första problemet löses med väl beprövade, fasta och standardiserade metoder för randomisering, t. ex. dubbel-blind, matchning. Andra problemet styrs inte av lika fasta regler utan har mera karaktären av godtycke, vilket har stor betydelse för den medicinska nyttan av en studie. Enligt min mening har detta inte lyfts fram tillräckligt i den vetenskapliga debatten, varför jag avser att göra det här.
De undersökta variablerna kan vara både kontinuerliga eller icke-kontinuerliga respektive normalfördelade eller snedfördelade. Många mänskliga egenskaper, t. ex. längd och vikt, är både kontinuerliga och ’normalfördelade’ vilket grafiskt framställs med en Gauss-kurva och för vilka det finns väl beprövade test, t. ex. Student’s t-test. Då variablerna istället är snedfördelade eller icke-kontinuerliga, kan man använda sig av andra test, t. ex. icke-parametriska test eller chi2-analys.
Helt oavsett vilka statistiska test som passar för olika typer av undersökningar så bygger de alla emellertid på högst tre parametrar: 1. skillnad i medelvär-den eller frekvenser, 2. observationernas spridning runt medelvärdet och 3. antalet observationer.
I princip gäller följande:
1. ju större skillnad mellan medelvärden eller frekvenser, ju större antal observationer och ju mindre spridning – desto lättare uppnås statistisk signifikans.
2. Ju mindre skillnad mellan medelvärden eller frekvenser, ju färre observationer och ju större spridning – desto svårare att nå statistisk signifikans.
Härvid spelar precisionen i mätmetoden en mycket viktig roll eftersom dålig mätprecision ökar spridningen och således försvårar uppnåendet av statistisk signifikans.
För att underlätta den statistiska jämförelsen mellan två stickprov av kontinuerlig och normalfördelad karaktär görs två transformationer: 1. z-transformation av kurvan (= de olika mätvärdena placeras nu utefter x-axeln där talet 0 utgör det nya medelvärdet) och övriga observationer på en plus eller minussida av detta medelvärde, och 2. t-transformation av de olika mätvärdena enligt en t-tabell som ovan beskrivits och som visas på denna grafiska bild:
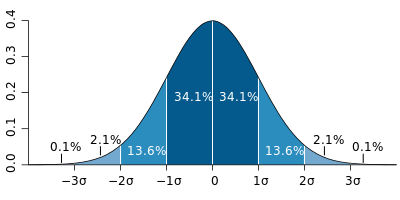
Under förutsättning att observationerna är slumpmässigt valda och oberoende av varandra kommer medelvärden och spridningsvärden redan efter 40-60 observationer att fördela sig som de skulle göra om observationerna omfattade flera tusen. Detta är välkänt för alla statistiker och själva grunden för tillförlitlig statistik även på små urval. T-tabellen (från Student’s T-test) visar t. ex. att 95 % av obser-vationerna (2,5 %- percentilen) hamnar inom intervallet ± 2,00 standardavvikelser redan efter 60 observationer och inom intervallet ± 1,98 standardavvikelser vid 120 observationer, dvs. en skillnad på endast 1 procent. Intervallet kan aldrig bli mindre än ± 1,96 standardavvikelser vilken helt konstanta spridning nås redan efter några hundra observationer.
[se t-fördelning t. ex.: http://www.maths.lth.se/matstat/kurser/tabeller/tabeller.pdf ].
I denna tabells vänstra kolumn står antalet frihetsgrader där frihetsgrader är antalet observationer minus 1, (y = n-1).
I mitt resonemang skall jag utgå ifrån ”Student’s t-test”, som används vid jämförelser mellan olika randomiserade mindre stickprov. Jag skall också längre ner i artikeln upprepa samma resonemang för chi2-testet, som rör jämförelser mel-lan frekvenser.
I. Student’s t-test lyder som följer:
Ekvation a-c i tur och ordning:
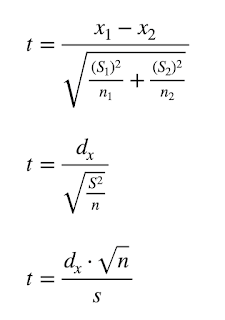
Här ser vi de tre viktiga parametrarna:
Ekvation (a):
1. differensen ”d” = (X1 – X2) mellan olika gruppers medelvärden, t. ex. placebo vs. försöksgrupp.
2. S1 och S2 representerar här spridningsmåttet ’standardavvikelsen’ och
3. n1 och n2 representerar antalet observationer i de båda grupperna.
När man skapat gemensam nämnare inom rottecknet kan formeln skrivas om som i ekvation b) och c). Det som jag avser att belysa syns tydligast i ekvation c).
t är här ett tal som varierar lite (men inte mycket) beroende på antalet observa-tioner. Talet t beskriver det intervall inom vilket 95 % av alla observationer i undersökningen kommer att hamna. I en t-tabell kan man avläsa att för 6o till oändligt många observationer kommer 95% av alla observationer att hamna inom intervallet från ± 2,00 till ± 1,96 standardavvikelser, dvs. en variation på endast cirka två procent. Det numeriska värdet på t är således i det närmaste helt kons-tant för antalet observationer flera än 60.
De två andra faktorerna, medelvärdena och standardavvikelserna blir praktiskt taget också konstanta redan efter 40-60 observationer. Vi har således en situation då en behandlingsmetod blir statistiskt signifikant om det bråk som står till höger om likhetstecknet överstiger värdet ≈ 1,98. Men eftersom skillnaden och standardavvikelsen praktiskt taget är konstanta så hänger hela ekvationen på talet n. Av denna anledning får det numeriska värdet på n en orättmätigt stor betydelse när det gäller den medi-cinska betydelsen av ett studieresultat och kan öka flera tusen procent vid stora jämfört med små studier. Talet n kommer därför i stora studier att fungera som kosmetika och dölja bristerna i försöks-designen. Vi ser i ekvation c) hur en hundra gånger så stor studie (t. ex 6.000 mot 60 observationer) kan statistiskt säkerställa en tio gånger så liten behandlingseffekt (=differensen) som i den mindre studien. Är detta vad vi vill uppnå?
Ett annat exempel: Antag att man genomfört en jämförande studie på 120 pati-enter, i vilken hälften fått ”verksam drog” och andra hälften ”placebo”. Antag vidare att jämförelsen inte uppnådde statistisk signifikans, och att en ”power-analys” visade att uppnående av statistisk signifikans skulle kräva minst 300 patienter och en inkludering av ytterligare 180 patienter. Vad skulle nu hända om forskarna istället för att inkludera ytterligare 180 patienter bara ändrade på talet n från 120 till 300 – dvs. ägnade sig åt fusk? Svar: Man skulle få exakt samma resultat! Inkludering av ytterligare patienter ändrar nämligen inte standardavvikelse, medelvärdena eller t – värde, annat än ytterst marginellt, eftersom alla dessa värden praktiskt taget är konstanta redan vid 60 – 120 observationer.
De flesta doktorer är säkert överens om att de 99%-, 95%- eller 90%-iga konfidensintervallen är valda på godtyckliga grunder. Men detta godtycke är en nödvändig förutsättning för den statistiska kalkylen. Utan ett valt konfidensintervall så kan man inte göra någon statistisk beräkning.Alla är dock säkert inte överens om eller kanske inte ens medvetna om att när man använder olika antal observationer och/eller olika grad av mätprecision i sina undersökningar så inför man ytterligare två godtyckliga element i beräkningarna, som kan ha större inflytande på bevisföringen än det valda konfidens-intervallet.
Jag övergår nu till icke-kontinuerliga och snedfördelade variabler.
II. Formeln för chi2-testet ser ut så här:
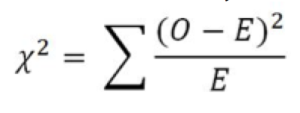
O står för observerad frekvens och E för förväntad frekvens.
Det kan t. ex. gälla antalet dödsfall i samband med en viss behandling av farlig sjukdom på en intensivvårdsavdelning. I en nyligen publicerad studie (Citrilus-studien) på 178 patienter, som inkommit till avdelningen i svår septisk chock, fick patienterna sedvanlig sepsis behandling med vätska och antibiotika. Hälften av dessa patienter (slumpvis utvalda) fick också i tillägg av Vitamin C 50 mg/kg som intravenösa infusioner 4 gånger per dag under 4 dagar (grupp A) medan andra hälften fick placebo infusioner i tillägg (grupp B). Efter 4 dagar hade endast 3 patienter i C-vitamingruppen (grupp A) dött medan 24 patienter dött i placebogruppen (grupp B). Med hjälp av en chi2-tabell får man fram att denna skillnad i mortalitet är statistiskt högsignifikant (p<0.005). Alltså: sannolikheten (p=probability) för att denna skillnad i mortalitet skulle bero på en slump – och inte C-vitaminet – är en chans på 200. [Chi2-tabell se: http://gauss.stat.su.se/gu/sg/Tabellchitva.pdf] Om man skulle gjort denna studie dubbelt så stor och involverat 356 patienter, så skulle man naturligtvis fått ungefär samma fördelning, dvs. 6 mot 48 döda i grupperna A och B, vilket i chi2 tabellen motsvaras av ett p-värde på < 0.00005.
Om man nu redan erhållit ett p-värde på 0.005 vad finns det då för anledning att göra en dubbelt så stor studie om detta endast resulterar i ett p-värde på 0.00005? Det är ju bara kosmetika. Ändå efterfrågar många doktorer större studier då man redan fått en klar statistiskt signifikant skillnad i en mindre studie?
Det finns 3 godtyckligt bestämda faktorer som påverkar bevisföringen i en vetenskaplig studie: 1. konfidensintervallet, 2. antalet observationer och 3. mätprecisionen. Under förutsättning att randomiseringen i ett vetenskapligt material är korrekt utförd så gäller följande:
1. Om en liten undersökning påvisar en statistiskt signifikant skillnad eller samband, så betyder detta både att skillnaden är stor eller sambandet klart och att antalet observationer samt mätprecisionen är tillräckliga för att bevisa detta. Då behövs ingen större studie för att konfirmera resultatet.
Om den lilla undersökningen emellertid misslyckas med att påvisa en skillnad eller ett samband, så utesluter inte detta att en skillnad eller ett samband föreligger utan kan bero på otillräckligt antal observationer, för dålig mätprecision eller en kombination av båda dessa. En sådant ”negativt” resultat får därför absolut inte användas för att motbevisa en studie, som redan påvisat en skillnad eller ett samband. Detta görs tyvärr ofta.
2. Om man måste göra en stor undersökning för att uppnå statistisk signifikans, så betyder detta att skillnaden är liten eller sambandet svagt. Man skall därför ha en viss skepsis inför stora studier och ha i bakhuvudet att dessa endast påvisar små skillnader och svaga samband.
Slutsats: Om det undersökta materialet är tillräckligt stort för en fullgod randomisering (80-120 oberoende observationer) så har man störst medicinsk nytta av en relativt liten studie om denna visar statistisk signifikans. Ju större studien blir utöver detta desto mindre behandlingseffekt och således desto mindre medicinsk nytta. Detta i bjärt kontrast mot en spridd missuppfattning inom massmedia och tyvärr också inom en stor del av läkarkåren att ju större studien är desto större medicinsk nytta.
Sture Blomberg